Noviembre


Funciones Vectoriales

Se llama función vectorial a cualquier función de la forma
donde las funciones componentes f, g y h son funciones del parámetro t con valores reales. Las funciones vectoriales se denotan con frecuencia por:


Debe quedar clara la distinción entre la función vectorial r y las funciones de variable real f, g y h. Todas son funciones de la variable real t, pero r (t) es un vector mientras que f (t), g (t) y h (t) son números (para cada valor especificado de t).


Las funciones vectoriales juegan un doble papel en la representación de curvas. Tomando como parámetro t el tiempo, las podemos usar para describir el movimiento a lo largo de una curva. Más en general, podemos usar una función vectorial para trazar la gráfica de una curva. En ambos casos, el punto final del vector posición r (t) coincide con el punto (x, y) o (x, y, z) de la curva dada por las ecuaciones paramétricas, como muestra la figura 11.1. La flecha sobre la curva indica el sentido de recorrido, es decir, el sentido de valores crecientes de t.
Salvo que se especifique otra cosa, se considera como dominio de una función vectorial r la intersección de los dominios de las funciones f, g y h. Por ejemplo el dominio de:

 es el intervalo (0, 1]

  


En la ciencia y la ingeniería a menudo es conveniente introducir un vector r con las funciones f y g como componentes.


R(t) = < f(t), g(t)> =f(t)i + g(t)j

Se dice que r es una función vectorial. De manera semejante, una curva en el espacio es parametrizada por 3 ecuaciones 

X = f(t) y = g(t) z = h(t) a " t " b

Una función vectorial se expresa como:

R(t) = < f(t),g(t), h(t) > = f(t) I +g(t) j + h(t)k

Triedro de Frenet

1. Definición del Método.

Sea T ⊂ R3 una curva y sean γ : I = [a, b] → R3, γ(t) = (x(t), y(t), z(t)) una
parametrización regular y α : I′ = [a′, b′] → R3 su parametrización respecto el
parámetro arco.
A partir de la primera y segunda derivada de la parametrización de la curva
se construye el triedro de Frenet. En cada punto regular de la curva γ(t), son
tres vectores unitarios y ortonormales, T(t), B(t) y N(t). Es decir, el triedro de
Frenet es un sistema de referencia ortonormal que nos proporciona
información sobre la curva. Decimos que es un sistema de referencia móvil,
porque se desplaza por la curva según la recorremos.
Foto4.jpg
A partir de los vectores del triedro de Frenet construiremos planos (el osculador, el normal y el rectificante). También introduciremos los conceptos de curvatura y torsión, que nos darán información de cómo se “dobla” y “retuerce” la curva en el espacio.
Para llegar calcular el Triedro de Frenet en cualquier punto de una curva, lo primero que debemos hacer es parametrizarla (en el caso de que no lo este). Una vez que hallamos parametrizado la curva en cuestión, generalmente mediante coordenadas polares, podemos comenzar a “construir” nuestro Triedro de Frenet.

2. Vector Tangente.

Lo primero que deberíamos hacer es calcular el vector Tangente del triedro, ya que sobre él están basadas todos los cálculos posteriores. Para calcularlo utilizaremos la siguiente fórmula:
T=r′(t)|r′(t)|
*Donde r (t) es el vector que define a nuestra curva ya parametrizada, r’(t) es su derivada y |r’(t)| es el módulo de la derivada.

3. Vector Normal Principal.

En segundo lugar debemos calcular el vector Normal Principal del triedro, para hallar su expresión usaremos esta fórmula:
N=T′(t)|T′(t)|
*Donde T’ (t) es la derivada del vector Tangente y | T’ (t) | es el módulo de la derivada.

4. Vector Binormal.

En último lugar para completar el Triedro de Frenet, tenemos la necesidad de hallar cual es el vector Binormal, el cual es normal al Vector Tangente y al Vector Normal Principal, de ahí que podamos calcularlo mediante un simple producto vectorial entre ambos vectores:
B = T x N

5. Longitud de la curva.

Otro apartado importante, que se ve junto con el Triedro de Frenet, es como poder llegar a calcular la longitud de la curva con la que estamos trabajando.
Generalmente, usaremos la siguiente expresión:
L=∫ba|r′(t)|dt
Sin embargo, un muchas ocasiones esta integral no posee una primitiva con la cual calcular el valor de L, por lo que deberemos usar Métodos de Integración Numérica para poder aproximar el valor de L. Todos estos métodos suelen dar valores muy cercanos al verdadero, con errores inferiores al 5%.
Uno de los métodos que, personalmente, recomiendo es La Regla del Trapecio, debido principalmente a la facilidad de su uso y de su recordatorio. La cual es la siguiente:
∫baf(x)dx∼b−a2(f(a)+f(b))
Otros métodos de integración numérica son estos:

6. Curvatura y Torsión.

Otra de las cosas que veremos en este apartado de la asignatura de Cálculo II, es la curvatura, así como el radio de curvatura, y también la torsión, todas ellas características propias de la curva que estamos estudiando.

6.1. Curvatura, radio de curvatura y círculo osculador.

La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice, que más grande es la curvatura. Su expresión es:
K=T′(t)|r′(t)|
De esta misma manera, definimos el radio de curvatura como la magnitud que mide la curvatura de un objeto geométrico, tal como una línea curva, una superficie o ,más en general, una variedad diferenciable definida en un espacio euclídeo. Su expresión es:
ρ=1K
En este apartado, además veremos el círculo osculador, que por así decirlo es el que “besa” a la curva en un punto dado. Una definición un poco más técnica sería esta: es una circunferencia cuyo centro se encuentra sobre la normal a la curva y tiene la misma curvatura que la curva dada en ese punto. El centro y el radio de la circunferencia osculatriz, en un punto de la curva, son llamados centro de curvatura y radio de curvatura de la curva en ese punto. El plano en el que está contenida la circunferecia osculatriz se denomina plano osculador.
foto5.jpg *Donde el radio de curvatura es ρ.

6.2. Torsión.

La torsión es una medida del cambio de dirección del vector binormal: cuanto más rápido cambia la torsión, más rápido gira el vector binormal alrededor del vector tangente y más retorcida aparece la curva. Por lo tanto, para una curva totalmente contenida en el plano, la torsión es nula, ya que, el vector binormal es constantemente perpendicular al plano que la contiene. Su expresión es:
τ=−N∗dBds=−T′(t)|T′(t)|∗T(t)∗N′(t)|r′(t)|
Foto6.jpg

7. Planos del Triedro de Frenet.

Por último, en este apartado de la asignatura, debemos aprender a calcular y a dominar los conceptos de plano Normal, Rectificante y Osculador.
Foto7.jpg
Como podemos ver en la imagen el Plano Normal es perpendicular al Vector Tangente, el Plano Rectificante es perpendicular al Vector Normal Principal y el Plano Osculador es normal al Vector Binormal. Sus expresiones son:
Plano Normal.
(X−r(t))∗T=0
Plano Rectificante.
(X−r(t))∗N=0
Plano Osculador.

(X−r(t))∗B=0

Función de dos variables

Una función de dos variables es una regla de correspondencia que asigna a cada pareja de números reales (x, y) un y sólo un número real z.
El conjunto de parejas ordenadas para las cuales la regla de correspondencia dá un número real se llama dominio de la función. El conjunto de valores z que corresponden a los pares ordenados se llama imagen o contradominio.
Una función de dos variables se denota usualmente con la notación
z = f (x, y)
Las variables x, y se llaman variables independientes, y z se llama variable dependiente.
La gráfica de una función de dos variables es el conjunto de puntos con coordenadas (x, y, z) en donde (x, y) está en el dominio de f y z = f (x, y).
Este conjunto de puntos forma una superficie en el espacio tridimensional.
Monografias.com
Monografias.com
En consecuencia, la grafica de una función f de dos variables es una superficie que consta de todos los puntos del espacio tridimensional cuyas coordenadas cartesianas están determinadas por las ternas ordenadas de números reales (x, y, z). Como el dominio de f es un conjunto de puntos del plano x, y, y puesto que cada par ordenado (x, y) del dominio de f corresponde a solo un valor de z, ninguna recta perpendicular al plano x,ypuede intersectar a la grafica de f en mas de un punto.

Ejemplo ilustrativo 1
La función f del ejemplo 1 es el conjunto de todos los pares ordenados de la forma (P, z) tales que
Monografias.com z=v25- x2 -y2
Por tanto, la grafica de f es la semiesfera en el plano x y por arriba de este cuyo centro es el origen y tiene radio 5. Esta semiesfera se muestra en la figura 1.
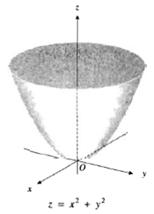
Monografias.com
Ejemplo 2: dibuje la grafica de la función
Sol/: la grafica de f es la superficie que tiene la ecuación z=x2 +y2 . La traza de la superficie en el plano x,y se obtiene al utilizar la ecuación z=0 simultáneamente con la ecuación de la superficie. Al hacerlo resulta x2 +y2=0 la cual representa el origen. Las trazas en los planos xz y yz se obtiene al emplear las ecuaciones z=x2 +y2. Estos trazos son las parábolas z= x2 y z= y2.
Monografias.com

Funciones de varias variables

El deseo de abordar problemas del mundo real, nos conduce a tomar en cuenta que, en general, cualquier situación o fenómeno requiere de más de una variable para su precisa descripción. Por ejemplo, el volumen de un cilindro depende del radio de la base y de su altura; la posición de un móvil en un momento determinado requiere para su exacta especiación, además del tiempo, de las tres coordenadas espaciales. Si adicionalmente se requiere la velocidad a la cual se desplaza, tendremos una función vectorial f que a cada vector de cuatro componentes (ubicación espacial y tiempo) le asigna la velocidad
V del móvil en ese punto y en ese instante:
f(x; y; z; t) = v
Observamos entonces que de acuerdo con la situación especifica que queramos describir, requerimos el tipo de función adecuada. Según si el dominio D y el rango R son subconjuntos de R; R2 o R3 las funciones se clasifican de la siguiente forma:
Función Nombre
Monografias.com
En cada caso, donde aparece R3 lo podemos sustituir por R2 y el nombre se conserva.
Las denominaciones escalar o vectorial se refieren a si la imagen de la función es un
numero o es un vector.

Ejemplo: la función g esta definida por
g (x, y, z) = x2+y2-z
entonces el paraboloide circular z= x2+y2, mostrado en la figura, es la superficie de nivel de g en 0. La superficie de nivel de g en el numero k tiene la ecuación z + k = x2 + y2 , un paraboloide circular cuyo vértice es el punto (0,0 –k) sobre el eje z. en al figura muestra las superficies de nivel para k igual a -4,-2, 0, 2 y 4


Método para hallar el dominio

Para hallar el dominio despejamos (y) y analizamos el comportamiento de (x). Al hacer este despeje podemos considerar tres casos:
  • i. La (x) hace parte del denominador de una fracción. Dé un ejemplo.R: Sea la relación R = {(x, y) / 2xy - 3y - 5 = 0} definida en los Reales.
  • ii. Despejar(y)



  • Monografias.com
    ¿Qué valores debe tomar (x) (en el denominador) para que sea diferente de cero?
    R/:
    Monografias.com
    Cómo se halla el dominio de una relación, cuando la (x) queda en el denominador al despejar (y).R: Si al despejar (y) en una expresión (en una relación), encontramos que la (x) hace parte del denominador de una fracción, entonces para determinar el dominio de dicha relación hay que hacer que el denominador sea diferente de cero y se despeja la (x).

    Método para hallar el Rango

    Como ya se dijo el rango es el conjunto formado por aquellos elementos del conjunto de llegada que están relacionados con algún elemento del conjunto de partida. Para encontrar el Rango de una relación en los reales, despejamos (x), analizamos el comportamiento de (y) y hacemos un análisis similar al que hicimos para encontrar el dominio.
    • Sea la relación R = {(x, y) / 3x2 + 4y2 = 12}, para ésta hallar el dominio y rango.Con sólo observar la ecuación diga ¿qué clase de relación real representa? ¿Por qué?
    R: Representa una elipse. Porque los coeficientes de x2 y de y2 son positivos y diferentes.
    Hallar el dominio.
    Monografias.com
    Vemos que la (x) hace parte de un radical par
    Monografias.com
    Solucionamos una desigualdad cuadrática
    Monografias.com
    Hallar el rango.R:Monografias.com
    La "y" hace parte de un radical par. Por lo tanto: 
    Monografias.com

    Curvas de nivel

    Cuando tenemos una función z = f(x, y) de dos variables reales y valor real, la gráfica de dicha función corresponde al conjunto gr (f):= {(x, y, f(x, y)): (X, y) ,¬ Dom (f)}. Al ubicar dichos puntos en el espacio R3, obtenemos una superficie en dicho espacio.
    Una forma de estudiar dicha superficie, aunque en dos dimensiones, es considerar la intersección de dicha superficie con el plano z = k, donde k ,¬ Recorrido (f). De esta manera, obtenemos el conjunto {(x, y, k): f(x, y) = k}, el cual corresponde a la curva de nivel de la superficie z = f(x, y) con z = k. Al proyectar dicha intersección en el plano
    x,y, obtenemos lo que se denomina curva de nivel.
    Cuando comparamos una superficie z = f(x, y) con una montaña, el estudio de las curvas de nivel corresponde a lo que acontece de manera análoga cuando dicha montaña es representada en dos dimensiones por medio de un mapa, donde se dibujan los contornos de dicha montaña indicando cual es la altura en las coordenadas (x, y) de dicho contorno.
    Monografias.com
    Ejemplo 1. Consideremos la función z = x2 + y2. Tomando k > 0, la curva de nivel correspondiente a z = k es la circunferencia x2 + y2 = k y tomando k = 0 la curva de nivel corresponde a la descrita por los puntos (x, y) tales que x2 + y2 = 0 (que corresponde únicamente al punto (0, 0))
    Monografias.com
    Sea g(x, y) = vxy la media geométrica de los números x e y. La curva de nivel 4 está formada por todos los pares de ordenados (x, y), la media geométrica de los cuales es 4.
    Por ejemplo, (4, 4), (2, 8) y (8, 2) están todos sobre esta curva de nivel. A continuación mostramos la gráfica de vxy y sus curvas de nivel en el plano xy.
    Monografias.com
    Consideramos ahora la función f(x, y) = x2 + y2. La curva de nivel 4 está formada por
    todos los pares (x, y) que cumplen:
    f (x, y) = x2 + y2 = 4.
    Puede que algunos de vosotros hayáis visto antes que la ecuación describe la circunferencia de radio 2(2 =v4) centrada en el origen de coordenadas.
    A continuación mostramos la gráfica de x2 + y2, así como diferentes curvas de nivel de la función.
    Monografias.com
    Así pues, podemos resumir:
    Dada una función f con dominio en R2 y un número cualquiera c, la curva de nivel c de la función f está formada por el conjunto de puntos que satisfacen f(x1, x2) = c.

  • Límites en funciones vectoriales

    La definición de límite es análoga a la del caso real y la generaliza. Dada una función vectorial, $f\colon I\to \mathbb{R}^m$, $a\in I\subset \mathbb{R}$ un punto de acumulación (es decir, que hay puntos del dominio tan cerca de $a$ como queramos), y $v\in\mathbb{R}^m$, decimos que $v$ es el límite de $f$ cuando $t$ tiende a $a$, ${\displaystyle \lim_{t\to a}f(t)=v }$, si ocurre que 
    \begin{displaymath}\forall \epsilon >0, \exists \delta >0\mbox{ tal que } \mid \mid f(t)-v \mid \mid <\epsilon\mbox{ si }0< \mid t-a \mid <\delta\end{displaymath}
    Como la norma en el caso $\mathbb{R}^m=\mathbb{R}$ coincide con el valor absoluto, esta definición generaliza a la que conocemos de $\mathbb{R}$ en $\mathbb{R}$. 

    Funciones componentes

    Si $f\colon\mathbb{R}\to \mathbb{R}^m$ es una función vectorial, $f(t)$ es un vector de $\mathbb{R}^m$, $f(t)\in \mathbb{R}^m$, y tiene coordenadas $f(t)=(f(t)_1,f(t)_2,\cdots ,f(t)_m)$. Cada coordenada $f(t)_i$ determina una función $f_i\colon\mathbb{R}\to\mathbb{R}$, $t\mapsto f_i(t):=f(t)_i$. A estas funciones se las denomina funciones componentes de $f$ y escribimos $f=(f_1,f_2,\cdots ,f_m)$
    El problema de calcular límites se reduce al calculo de sus componentes 

    Proposición

    Sea $f=(f_1,f_2,\cdots ,f_m)\colon\mathbb{R}\to \mathbb{R}^m$ y $v=(v_1,v_2,\cdots ,v_m)\in\mathbb{R}^m$ 
    \begin{displaymath}\lim_{t\to a}f(t)=v \iff \lim_{t\to a}f_i(t)=v_i ,\quad i=1,2\cdots ,m\end{displaymath}

    Continuidad de funciones vectoriales

    La continuidad se define como en el caso de una variable. Si $a$ es del dominio de $f$, $f\colon\mathbb{R}\to \mathbb{R}^m$, $f$ se dice que es continua en $x=a$ si ocurre que existe ${\displaystyle \lim_{t\to a}f(t) }$ y coincide con $f(a)$, 
    \begin{displaymath}\lim_{t\to a}f(t)=f(a)\end{displaymath}

    Como nos podemos reducir a las funciones componentes, resulta que $f$ es continua en $a$ si y solo si cada función componente $f_i$ es continua en $a$. 
    \begin{displaymath}f(a)=(f_1(a),f_2(a),\cdots ,f_m(a))\in \mathbb{R}^m\end{displaymath}


    \begin{displaymath}\lim_{t\to a}f(t)=f(a)\iff \lim_{t\to a}f_i(t)=f_i(a) ,\quad i=1,2,\cdots , m\end{displaymath}

    Ejemplos:

    $(1)$ $f(t)=(t^2,t+1)$ es continua en todo $\mathbb{R}$ ya que $f_1(t)=t^2$ y $f_2(t)=t+1$ lo son.
    $(2)$ ${\displaystyle g(t)=(\sqrt{t},\frac{ \mbox{ sen }t}{t}) }$ si $t\neq 0$ y $g(0)=(0,0)$.

    \begin{displaymath}g_1(t)=\cases{\displaystyle{\sqrt{t}, t\neq 0}&\cr 0 , t=0&}=... ...\frac{ \mbox{ sen }t}{t}, t\neq 0}&\cr&\cr \quad 0 ,\quad t=0&}\end{displaymath}

    $g$ es continua en $\mathbb{R}^*$, pero no en $t=0$ ya que 
    \begin{displaymath}\lim_{t\to 0}g(t)=(0,1)\neq g(0)\end{displaymath}

    Fijémonos que $g_2$ no es continua en $0$.
    $(3)$ ${\displaystyle h(x)=(\frac{x^2-1}{x-1},\frac{ \mbox{ sen }(x^2-1)}{x^2-1}) }$ si $x\neq 1$, $x\neq 1$; $h(1)=(2,1,2)$, $h(-1)=(0,0,0)$.
    $h_1$ es continua en todo $\mathbb{R}$ y $h_3$ también, pero $h_2$ no es continua en $x=-1$ ya que 
    \begin{displaymath}\lim_{x\to -1}\frac{x^2-1}{x-1}=1\neq 0=h_2(-1)\end{displaymath}


  • DERIVADAS PARCIALES 

      Sea una función de dos variables z = f(x, y), se definen las derivadas parciales:
    devv1.gif (940 bytes)
    (Una definición obvia si la comparamos con la derivada de una función de una variable)
      Para la derivada de z "respecto de x" consideramos a la variable "y" como si fuera una constante, mientras que al hacer la derivada de z "respecto de y" consideramos a la variable "x" como si fuera constante.
      Veamos, como ejemplo, las dos derivadas parciales de la función:   devv2.gif (119 bytes)  :
      Para ello recordemos que la derivada de la función  z = eu  es:   z’ = u’ . eu , siendo u en nuestro caso: x2 + y2 , entonces la derivada de u respecto x es 2x (con la y constante), mientras que laderivada de u respecto y es 2y (con la x constante). Así tenemos:
    devv3.gif (426 bytes)
      Otras formas de expresar la derivada de la función z = f(x,y) con respecto a x son:
    devv4.gif (215 bytes)
    mientras que para expresar la derivada de la función z = f(x,y) con respecto a y :
    devv5.gif (223 bytes)
      Esta definición de derivada se extiende a funciones de tres o más variables, por ejemplo, para una función de tres variables  w = f(x,y,z) sus tres derivadas parciales son:
    devv6.gif (530 bytes)
    devv7.gif (544 bytes)
    devv8.gif (520 bytes)
    en cada una de ellas se consideran constantes los dos parametros distintos a los que se realiza la derivada.
     Diferencial de una función de varias variables

    Sea una función de dos variables z = f(x, y), se define la diferencial de esta función como:
    devv9.gif (332 bytes)
    Geométricamente hay que interpretar las diferenciales como "incrementos infinitesimales".
    Como ejemplo, expresemos la diferencial de la función:  devv2.gif (119 bytes)  , ya que hemos realizado anteriormente las dos derivadas parciales:
    devva.gif (347 bytes)
      Tanto en las derivadas como en las diferenciales, se suele hablar de valores en un punto P(a, b), para ello se sustituye en ellas el valor de x por a, y el valor de y por b. Por ejemplo, las derivadas y la diferencial en el punto P(1, 2) se calculan sustituyendo x=1, y=2.
      Para la función devv2.gif (119 bytes) las derivadas en el punto P(1, 2) son:
    devvb.gif (558 bytes)
    y la diferencial en ese punto:
    devvc.gif (310 bytes)
    Diferencial de una función de varias variables.
    Sea una función de dos variables z = f(x, y), se define la diferencial de esta función como:
    devv9.gif (332 bytes)
    Geométricamente hay que interpretar las diferenciales como "incrementos infinitesimales".
    Como ejemplo, expresemos la diferencial de la función:  devv2.gif (119 bytes)  , ya que hemos realizado anteriormente las dos derivadas parciales:
    devva.gif (347 bytes)
      Tanto en las derivadas como en las diferenciales, se suele hablar de valores en un punto P(a, b), para ello se sustituye en ellas el valor de x por a, y el valor de y por b. Por ejemplo, las derivadas y la diferencial en el punto P(1, 2) se calculan sustituyendo x=1, y=2.
      Para la función devv2.gif (119 bytes) las derivadas en el punto P(1, 2) son:
    devvb.gif (558 bytes)
    y la diferencial en ese punto:
    devvc.gif (310 bytes)

        Derivadas parciales de segundo orden.
      Sea una función de dos variables z = f(x, y). En principio tenemos cuatro (22) derivadas de segundo orden:
    devvd.gif (480 bytes)
    (se debe leer  "derivada segunda de z respecto de x dos veces", "derivada segunda de z respecto de x-y", etc.)
      Estas derivadas vienen definidas de la siguiente manera:
     devve.gif (1295 bytes)
      Se trata de derivar respecto de x la derivada devvf.gif (109 bytes).
      Se trata de derivar respecto a x la derivada devvg.gif (110 bytes).
       Se trata de derivar respecto a y la derivada devvf.gif (109 bytes).
       Se trata de derivar respecto a y la derivada  devvg.gif (110 bytes).
      Siguiendo con nuestro ejemplo, calculemos estas derivadas para la función devv2.gif (119 bytes):
    devvh.gif (1153 bytes)
      Las derivadas devvi.gif (285 bytes) son llamadas "derivadas mixtas", obsérvese en el ejemplo cómo estas derivadas son iguales, lo cual no es una coincidencia sino el resultado de un teorema que vamos a pasar a ver.

  • Adjunto estos videos para reforzar el conocimiento:



1 comentario:

Suscribirse a: Entradas (Atom)