DERIVADA PARCIALES
diversas variables, es su derivada respecto a una de esas
variables manteniendo las otras como constantes. Las
derivadas parciales son
La derivada parcial de una función f respecto a la
variable x se representa con cualquiera de las
siguientes notaciones equivalentes:
Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'. es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Cuando una magnitud  es función de diversas variables ( es función de diversas variables ( , , , , , , ), es decir: ), es decir:
Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función  en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z. en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
Introducción
Supongamos que  es una función de más de una variable, es decir una función real de variable vectorial. Para el caso, es una función de más de una variable, es decir una función real de variable vectorial. Para el caso,

Un gráfico de z = x2 + xy + y2. Queremos encontrar la derivada parcial en (1, 1, 3) que deja a yconstante; la correspondiente línea tangente es paralela al eje x.
Es difícil describir la derivada de tal función, ya que existe un número infinito de líneas tangentes en cada punto de su superficie. La derivación parcial es el acto de elegir una de esas líneas y encontrar su pendiente. Generalmente, las líneas que más interesan son aquellas que son paralelas al eje x, y aquellas que son paralelas al eje y.

Este es un corte del gráfico de la derecha dondey = 1.
Una buena manera de encontrar los valores para esas líneas paralelas es la de tratar las otras variables como constantes mientras se deja a variar sólo una. Por ejemplo, para encontrar la línea tangente de la función de arriba en (1, 1, 3) que es paralela el eje x, tratamos a la variable y como constante. El gráfico de la función y el plano y = 1 se muestran a la derecha. A la izquierda, vemos cómo se ve la función, en el plano y = 1. Encontrando la línea tangente en este gráfico, descubrimos que la pendiente de la línea tangente de ƒ en (1, 1, 3) que es paralela al eje x es tres. Que escribimos:
en el punto (1, 1, 3),
o como "La derivada parcial de z con respecto a x en (1, 1, 3) es 3."
Ejemplos
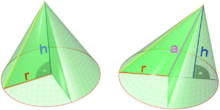
El volumen de un cono depende de la altura (h) y el radio (r)
- Considera el volumen V de un cono, este depende de la altura h del cono y su radio r de acuerdo con la fórmula
Las derivadas parciales de V respecto a r y h son:
- Otro ejemplo, dada la función
 tal que: tal que:

la derivada parcial de  respecto de respecto de  es: es:
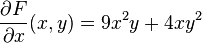
mientras que con respecto de  es: es:
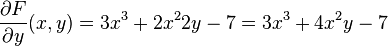
Definición formal
Como las derivadas en una variable, las derivadas parciales están definidas como el límite. Donde U es un subconjunto abierto de Rn y f : U → R una función. Definimos derivada parcial de f en el punto a = (a1,..., an) ∈ U con respecto a la i-ésima variable xi como:
O visto respecto a la derivada direccional:
donde 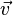 es el vector unitario del eje respecto al que se deriva ( es el vector unitario del eje respecto al que se deriva ( ). ).
Incluso si todas las derivadas parciales existen en el punto a, la función no necesariamente es continua en ese punto. Sin embargo, si todas las derivadas parciales existen alrededor de a y son continuas, entonces la función no sólo es continua sino además diferenciable cerca de a. En este caso, f es una función C1.
Notación
Para el siguiente ejemplo, f será una función de x e y.
- Derivadas parciales de primer orden:
Derivadas parciales (dobles) de segundo orden:
Derivadas cruzadas de segundo orden:
Termodinámica
En termodinámica y otras áreas de la física se emplea la siguiente notación:
Que significa que  y entonces: y entonces:
Esta notación se usa porque frecuentemente una magnitud puede expresarse como función de diferentes variables por lo que en general:
Ya que la forma precisa de las funciones  y y  es diferente, es decir, se trata de funciones diferentes. es diferente, es decir, se trata de funciones diferentes.
Derivadas parciales de orden superior
A su vez, la derivada parcial  puede verse como otra función definida en U y derivarse parcialmente. Si todas sus derivadas parciales existen y son continuas, llamamos a f una función C2; en este caso, las derivadas parciales (llamadas parciales) pueden ser intercambiadas por el teorema de Clairaut también conocido como teorema de Schwarz. puede verse como otra función definida en U y derivarse parcialmente. Si todas sus derivadas parciales existen y son continuas, llamamos a f una función C2; en este caso, las derivadas parciales (llamadas parciales) pueden ser intercambiadas por el teorema de Clairaut también conocido como teorema de Schwarz.
En R2, si se cumple lo ya dicho, se asegura que:
Derivadas parciales de orden superior
Lo mismo que sucede con las derivadas ordinarias, es posible encontrar derivadas parciales de una función de varias variables de órdenes segundo, tercero y superiores, supuesto que tales derivadas existen. Denotamos las derivadas de orden superior por su orden de derivación. Por ejemplo, hay cuatro formas distintas de encontrar una derivada parcial segunda de z=f(x,y).
1. Derivar dos veces respecto de x:
2. Derivar dos veces respecto de y:
3. Derivar primero con respecto a x y luego con respecto a y:
4. Derivar primero con respecto a y y luego con respecto a x:
Los casos tercero y cuarto se conocen como derivadas parciales cruzadas. Se debe observar que hay tipos de notación para las derivadas parciales cruzadas, según convenio se utilice para indicar el orden de derivación. Así, la parcial
 Orden de derecha a izquierda Orden de derecha a izquierda
indica que la primera derivación es con respecto a x, pero la parcial
(fy)x=fyx Orden de izquierda a derecha
indica que la primera derivación es con respecto a y. Observar que con ambas notaciones se drivaprimero respecto de la variable que está más cercana a f.
Ejemplo
Encontrar las derivadas parciales segundas de  y calcular el valor de fxy(-1,2) y calcular el valor de fxy(-1,2)
Solución
Primero calculemos las derivadas parciales primeras con respecto a x y a y:
Y derivando cada una de estas con respecto a x y a y, resulta
Finalmente, fxy(-1,2)=12-40=-28
Se observa que las derivadas parciales cruzadas son iguales. Esto sucede frecuentemente, como se indica en teorema siguiente.
Teorema 3.1
Si f es una función de x e y tal que f, fx, fy, fxy y fyx son continuas en la región abierta R, entonces para cada (x,y) en R,
|
Ejemplo
Probar que las derivadas parciales cruzadas son iguales para la función 
Solución
Las parciales primeras son,
Y las parciales cruzadas son,
Diferenciales
En este capítulo generalizamos los conceptos de incrementos y diferenciales a funciones de dos o más variables. Para una función de dos variables, dada por z=f(x,y), usamos una terminología similar a las de las funciones de una variable. Llamamos  y y  a los incrementos de x y de y, y el incremento de z viene dado por a los incrementos de x y de y, y el incremento de z viene dado por
Las diferenciales dx, dy y dz se definen como sigue.
Definición
Si z=f(x,y) y  , , son incrementos de x y de y, entonces las diferenciales de las variables independientes x e y son son incrementos de x y de y, entonces las diferenciales de las variables independientes x e y son
dx= y dy= y dy= 
y la diferencial total de la variable dependientee z es
|
Ejemplo
La diferencial total dz para la función  es es
En el cálculo de una variable se tiene que para una función diferenciable dada por y=f(x), podemos usar la diferencial dy=f´(x) dx como una aproximación (para  pequeños) al valor pequeños) al valor  . Cuando es posible una aproximación similar para una función de dos variables, decimos que esdiferenciable. A continuación se anuncia esto explícitamente en la definición 4.2. . Cuando es posible una aproximación similar para una función de dos variables, decimos que esdiferenciable. A continuación se anuncia esto explícitamente en la definición 4.2.
Diferenciabilidad
Definición
Una función f dada por z=f(x,y) es diferenciable en (x,y) si  puede expresarse en la forma puede expresarse en la forma
donde ambos  cuando cuando  . Se dice que la función f es diferenciable en la región R si es diferenciable en todo punto de R. . Se dice que la función f es diferenciable en la región R si es diferenciable en todo punto de R. |
Ejemplo
Probar que la función  es diferenciable en todos los puntos del plano. es diferenciable en todos los puntos del plano.
Solución
Haciendo z=f(x,y), el incremento de z en un punto arbitrario (x,y) del plano es
donde  . Como . Como  cuando cuando  , entonces f es diferenciable en todo punto del plano. , entonces f es diferenciable en todo punto del plano.
| Observar que el término diferenciable se usa de forma distinta al aplicarlo a funciones de dos variables y a funciones de una variable. Una función de una variable es diferenciable en un punto si su derivada en ese punto existe. Sin embargo, para una función de dos variables la existencia de las derivadas parciales fx y fy no garantiza que la función sea diferenciable. (ver Ejemplo 4.5). En el teorema siguiente, presentamos una condición suficiente para la diferenciabilidad de una función de dos variables. |
Aproximación por diferenciales
Teorema
| Si f es una función de x e y, con f, fx y fy continuas en una región abierta R, entonces f esdiferenciable en R. |
Este teorema nos dice que podemos elegir (x+ ,y+ ,y+ ) suficientemente próximos a (x,y) para hacer ) suficientemente próximos a (x,y) para hacer  insignificantes. En otras palabras, para insignificantes. En otras palabras, para  y y  pequeños podemos usar la aproximación pequeños podemos usar la aproximación
Recordemos que las derivadas parciales pueden interpretarse como las pendientes de la superficie en las direcciones x e y, respectivameente. Esto significa que
representa la variación en altura de un plano tangente a la superficie en el punto (x,y,f(x,y)). Puesto que un plano del espacio se representa por una ecuación lineal en las variables x, y ,z, llamamos a esta aproximación de  por dz aproximación lineal. por dz aproximación lineal.
Ejemplo
Usar la diferencial dz para aproximar la variación en  cuando (x,y) va desde el punto (1,1) a (1.01,0.97). Comparar esta aproximación con la variación exacta de z. cuando (x,y) va desde el punto (1,1) a (1.01,0.97). Comparar esta aproximación con la variación exacta de z.
Solución
Haciendo (x,y)=(1,1) y (x+ ,y+ ,y+ )=(1.01,0.97) tenemos que )=(1.01,0.97) tenemos que
dx= =0.01 y dy= =0.01 y dy= =-0.03 =-0.03
luego la variación en z puede aproximarse por
En x=1 e y=1, resulta
Ahora calculamos la variación exacta  (observe que la diferencia es mínima) (observe que la diferencia es mínima)
Esta teoría se extiende la funciones de tres variables como se ve en el siguiente ejemplo.
Ejemplo
El posible error involucrado al medir cada una de las dimensiones de una caja rectangular es de  0.1 milímetros. Las dimensiones de la caja son x=50 centímetros, y=20 centímetros y z=15 centímetros. Utilizar dV para estimar el error propagado y el error realativo en el volumen calculado de la caja. 0.1 milímetros. Las dimensiones de la caja son x=50 centímetros, y=20 centímetros y z=15 centímetros. Utilizar dV para estimar el error propagado y el error realativo en el volumen calculado de la caja.
Solución
El volumen de la caja viene dado por V=xyz, luego
Como 0.1 milímetros es igual a 0.01 centímetros, tenemos que dx=dy=dz= 0.01 y el error propagado es 0.01 y el error propagado es
Puesto que el volumen es V=(50)(20)(15)=15000 centímetros cúbicos, el error relativo es
Al igual que ocurre con las funciones de una variable, si una función de dos variables es diferenciable en algún punto de su dominio, entonces tanbién es continua en dicho punto. Este es el contenido del siguiente teorema:
Teorema 4.2
| Si una función de x e y es diferenciable en (x0,y0), entonces es continua en (x0,y0). |
Ya hemos señalado que la existencia de las derivadas parciales primeras no es suficiente para garantizar la diferenciabilidad. En el ejemplo siguiente usamos el teorema 4.2 para mostrar su validez.
Ejemplo
Mostrar que existen ambas fx(0,0) y fy(0,0), pero que f no es diferenciable en (0,0), estando f definida como
Solución
Por el teorema 4.2 podemos ver que f no es diferenciable en (0,0) si no es continua en dicho punto. Para ver que f no es continua en (0,0), nos fijamos en los valores de (x,y) cerca de (0,0), pero según dos direcciones diferentes, como se indica en la figura 4.1. Por la recta y=x, el límite es
mientras que pot y=-x tenemos que
figura 4.1
Luego el límite de f(x,y) cuando (x,y) se aproxima a (0,0) no exisite, y concluimos que f no es continua en (0,0). Por tanto, por el teorema 4.2 sabemos que f no es diferenciable en (0,0). Por otro lado, por la definición de las derivadas parciales fx y fy tenemos
luego las derivadas parciales en (0,0) existen.
Regla de la Cadena
El trabajo con diferenciales nos proporciona la base para la extensión de la regla de la cadena a funciones de dos variables. en esta extensión, consideramos dos casos. En el primero interviene w como función de x e y, donde x e y son funciones de una única variable independiente t.
Teorema
Sea w=f(x,y), donde f es una función diferenciable de x e y. Si x=g(t) e y=h(t), siendo g y h funciones de t, entonces w es una función derivable de t, y
|
Ejemplo
Sean  , donde , donde  . Encontrar dw/dt cuando t=0. . Encontrar dw/dt cuando t=0.
Solución
Por la regla de la cadena para una variable independiente tenemos
Cuando t=0, x=0 e y=1, entonces dw/dt=0-2=-2.
La regla de la cadena presentada en esta sección nos proporciona técnicas alternativas de solución para muchos problemas del cálculo con una sola variable. Así en el ejemplo 4.6, podríamos haber utilizado técnicas de una sola variable para hallar dw/dt escribiendo en primer lugar w como función de t,
y a continuación derivando en forma usual.
La regla de la cadena en el teorema 4.3 puede extenderse a un número cualquiera de variables. Por ejemplo, si cada xi es función derivable de una sola variable t, entonces para w=f(x1,x2, ..., xn) tenemos
Otro tipo de función compuesta es aquel en que las variables intermedias son ellas mismas funciones de más de una variable. Por ejemplo, si
w=f(x,y)
donde
x=g(s,t) e y=h(s,t)
entonces se sigue que w es función de s y de t, y podemos considerar las derivadas parciales de w con respecto a s y a t. Una forma de encontrar estas derivadas parciales consiste en escribir w como función de s y de t explícitamente mediante la sustitución de las ecuaciones x=g(s,t) e y=h(s,t) en la ecuaciónw=f(x,y). Entonces, es posible hallar las derivadas parciales en la forma usual, como se muestra en el ejemplo siguiente
Ejemplo
Hallar  para w=2xy, donde para w=2xy, donde 
Solución
Comenzamos sustituyendo  en la ecuación w=2xy para obtener en la ecuación w=2xy para obtener
Entonces, para encontrar  mantenemos t constante y derivamos con respecto a s: mantenemos t constante y derivamos con respecto a s:
De forma similar, para hallar  mantenemos s constante y derivamos con respecto a t para obtener mantenemos s constante y derivamos con respecto a t para obtener
El teorema 4.4 nos proporciona un método alternativo para encontrar las derivadas parciales del ejemplo 4.7, sin tener que escribir explícitamente w como función de s y t.
Teorema 4.4
Sea w=f(x,y), donde f es una función diferenciable de x e y. Si x=g(s,t) e y=h(s,t), de forma tal que las derivadas parciales primeras  existen todas, entonces existen todas, entonces  existen y vienen dadas por existen y vienen dadas por
|
Las cadenas mencionadas en los teoremas 4.3 y 4.4 pueden representarse en forma de diagrama, como muestran las figuras 4.2 y 4.3 respectivamente.
figura 4.2
figura 4.3
Ahora podemos usar la regla de la cadena enuncuada en el teorema 4.4 para encontrar las mismas derivadas parciales calculadas en el ejemplo 4.7
Ejemplo
Usar la regla de la cadena para encontrar  para w=2xy, donde para w=2xy, donde  . .
Solución
Si fijamos t, entonces por el teorema 4.4,
En forma similar, fijando s obtenemos
La regla de la cadena del teorema 4.4 puede extenderse a un número cualquiera de variables. Por ejemplo, si w es una función diferenciable de n variables x1,x2, ..., xn, donde cada xi es una funcióndiferenciable de m variables t1,t2, ..., tm , entonces w=f(x1,x2, ..., xn) tenemos
Derivación parcial implícita
Finalizamos esta unidad con una aplicación de la regla de la cadena para determinar la derivada de una función definida implícitamente. Supongamos que x e y están relacionadas mediante la ecuación F(x,y)=0, donde se supone que y=f(x) es una función derivable de x. Para hallar dy/dy consideramos la función
w=F(x,y)=F(x,f(x))
entonces podemos aplicar el teorema 4.3 para obtener
Como w=F(x,y)=0 para todo x en el dominio de f, sabemos que dw/dx=0 y tenemos
Y si Fy(x,y) es distinto de cero, podemos concluir que
Un procedimiento similar puede usarse para encontrar las derivadas parciales de funciones de varias variables que se encuentran definidas implícitamente.
Teorema
a) Si la ecuación F(x,y)=0 define a y implícitamente como función de x, entonces
b) Si la ecuación F(x,y,z)=0 define a z implícitamente como función de x e y, entonces
|
Este teorema puede extenderse a funciones diferenciables definidas implícitamente con un número cualquiera de variables.
Ejemplo
Calcular dy/dx, sabiendo que  . .
Solución
Definimos una función F mediante
Usando el teorema 4.5 tenemos
luego
Ejemplo
Calcular  , sabiendo que , sabiendo que 
Solución
Para aplicar el teorema 4.5 definimos
entonces
Por lo tanto,
Derivadas parciales y diferenciales de órdenes superiores
Se llaman derivadas parciales de segundo orden de la función z = f(x,y) a las derivadas parciales de las derivadas parciales de primer orden.
Se usan las siguientes notaciones:
 ; ; 
 ; ;
(se empieza derivando por la variable que está más cerca de la función)
Si las derivadas parciales son continuas, entonces las derivadas cruzadas son iguales.
Igual se definen las derivadas parciales de tercer orden y de órdenes superiores.
Si las derivadas parciales son continuas entonces no dependen del orden en que se realicen, sino del número de veces que se derive respecto de cada una de las variables (aunque el resultado final sea igual, el cálculo puede resultar más complicado en un orden que en otro).
Se llama diferencial de segundo orden de una función a la diferencial de su diferencial total:
Análogamente se define la diferencial de tercer orden.
Se siguen unas reglas parecidas a las potencias:
Derivada de funciones implícitas
La derivada de la función implícita definida mediante la ecuación definida mediante la ecuación  puede calcularse: o bien despejando la y , o bien, mediante la siguiente fórmula: puede calcularse: o bien despejando la y , o bien, mediante la siguiente fórmula:
 , siempre que , siempre que 
Las derivadas de orden superior de una función implícita se pueden calcular mediante la derivación sucesiva de la fórmula anterior, considerando y como función de x.
Las derivadas parciales de una función implícita de dos variables  definida mediante la ecuación definida mediante la ecuación  puede calcularse mediante las fórmulas: puede calcularse mediante las fórmulas:
Dada la ecuación  Si el punto Si el punto  cumple la ecuación cumple la ecuación  , la función F tiene derivadas parciales continuas en un entorno de , la función F tiene derivadas parciales continuas en un entorno de  y y  entonces la ecuación entonces la ecuación  define una función explícita define una función explícita  en un entorno de en un entorno de con con
Dada la ecuación  Si el punto Si el punto  cumple la ecuación cumple la ecuación  , la función F tiene derivadas parciales continuas en un entorno de , la función F tiene derivadas parciales continuas en un entorno de  y y  entonces la ecuación entonces la ecuación  define una función explícita define una función explícita  en un entorno de dicho punto. en un entorno de dicho punto.
Derivada de la función compuesta
Entonces la derivada de la función compuesta  se puede calcular: o bien haciendo la sustitución, o bien, aplicando la siguiente fórmula: se puede calcular: o bien haciendo la sustitución, o bien, aplicando la siguiente fórmula:
Si  , donde , donde  , entonces la derivada total de z respecto de x se puede calcular: o bien haciendo la sustitución, o bien, aplicando la siguiente fórmula: , entonces la derivada total de z respecto de x se puede calcular: o bien haciendo la sustitución, o bien, aplicando la siguiente fórmula:
Si  , donde , donde  , , entonces las derivadas parciales se pueden calcular mediante las siguientes fórmula: entonces las derivadas parciales se pueden calcular mediante las siguientes fórmula:
 : :
|
|
Adjunto estos videos para mayor comprension:
|
|
0 comentarios:
Publicar un comentario