Derivada Direccional
En el análisis matemático, la derivada direccional de una
función multivariable sobre un vector dado, representa la
tasa de cambio de la función en la dirección de dicho vector.
Este concepto generaliza a las derivadas parciales, ya que
estas son derivadas direccionales en los vectores paralelos
a los ejes.
Definición
Definición general
La derivada direccional de
una función escalar:
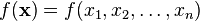
en la dirección del vector:

es la función definida por
el límite:
Si la función es diferenciable,
puede ser escrita en término de
su gradiente 

donde " " denota el producto
" denota el producto
 " denota el producto
" denota el producto
escalar o producto
punto entre vectores. En
cualquier punto  , la
, la
 , la
, la
derivada direccional de f
representa intuitivamente la
tasa de cambio de f
con respecto al tiempo cuando se está
moviendo a una velocidad y dirección dada por  en dicho
en dicho
 en dicho
en dicho
punto.
Definición solo en la dirección de un vector
Algunos autores definen la derivada direccional con
respecto al vector  después de la normalización, ignorando
después de la normalización, ignorando
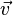 después de la normalización, ignorando
después de la normalización, ignorando
así su magnitud. En este caso:
Si la función es diferenciable, entonces
Esta definición tiene algunas desventajas: su aplicabilidad
está limitada a un vector de norma definida y no nula.
Además es incompatible con la notación empleada en otras
ramas de la matemática, física e ingeniería por lo que debe
utilizarse cuando lo que se quiere es la tasa de incremento
de  por unidad de distancia.
por unidad de distancia.
 por unidad de distancia.
por unidad de distancia.Restricción al vector unitario
Algunos autores restringen la definición de la derivada
direccional con respecto a un vector unitario. Con esta
restricción, las dos definiciones anteriores se convierten en
una misma.
Demostración
El caso más sencillo de la derivada direccional se da en el
espacio tridimensional. Supóngase que existe una función
diferenciable  . La derivada direccional según la
. La derivada direccional según la
 . La derivada direccional según la
. La derivada direccional según la
dirección de un vector unitario  es:
es:
 es:
es:El primero de estos límites puede calcularse mediante el
cambio  lo cual lleva, por ser diferenciable la
lo cual lleva, por ser diferenciable la
 lo cual lleva, por ser diferenciable la
lo cual lleva, por ser diferenciable la
Procediendo análogamente para el otro límite se tiene que:
Resultado que trivialmente coincide con el producto
escalar del gradiente por el vector  :
:
 :
:Notaciones alternas
La derivada direccional puede ser denotada mediante los
símbolos:
donde  es la parametrización de una curva para la cual
es la parametrización de una curva para la cual 
 es la parametrización de una curva para la cual
es la parametrización de una curva para la cual 
es tangente y la cual determina su magnitud.
Propiedades
Muchas de las propiedades conocidas de las derivadas se
mantienen en las derivadas direccionales. Estas incluyen,
para cualquier pareja de funciones  y
y  definidas en
definidas en
 y
y  definidas en
definidas en
la vecindad de un punto  , donde son diferenciables:
, donde son diferenciables:
 , donde son diferenciables:
, donde son diferenciables:- Regla de la suma:
- Regla del factor constante:
donde  es cualquier constante.
es cualquier constante.
 es cualquier constante.
es cualquier constante.- Regla de la cadena: Si
 es diferenciable en el punto
es diferenciable en el punto  y
y 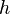 es diferenciable en
es diferenciable en  , entonces:
, entonces:
Campos vectoriales
El concepto de derivada direccional no se puede generalizar
a funciones de  en
en  , del tipo:
, del tipo:
 en
en  , del tipo:
, del tipo:
En este caso la derivada direccional de modo idéntico a
como se hacía con funciones de una variable:
Una diferencia con el caso de funciones de reales de una
variable es que la existencia de derivadas direccionales
según todas las direcciones no implica necesariamente que
una función sea diferenciable. Si la función es diferenciable
resulta que la aplicación:
Es lineal y se cumple además es expresable en términos
del jacobiano:
Funcionales
La derivada funcional, definida como derivada de Gâteaux,
es de hecho una derivada direccional definida en general
sobre un espacio vectorial de funciones.
Derivada direccional
Suponga que deseamos calcular la tasa de cambio de
En la liga [Ver en 3D-LG3D] de la figura1, se puede arrastrar con el mouse el punto  y/o el vector
y/o el vector  para observar como varía la tasa de cambio en
para observar como varía la tasa de cambio en  en la dirección de
en la dirección de 

Figura 1: derivada direccional en P en la dirección de u[Ver en 3D - LG3D][Ver en 3D - Jview]
Si  es otro punto sobre la curva
es otro punto sobre la curva  , y si
, y si  y
y  son las proyecciones sobre el plano
son las proyecciones sobre el plano  de los vectores
de los vectores  y
y  , entonces el vector
, entonces el vector  es paralelo al vector
es paralelo al vector  , y por consiguiente
, y por consiguiente

Figura 2: derivada direccional en P en la dirección de u
para algún escalar . Así pues,
. Así pues,
y la razón de cambio está dada por
y al tomar el límite cunado  obtenemos la tasa de cambio instantanea de
obtenemos la tasa de cambio instantanea de (con respecto a la distancia) en la dirección de
(con respecto a la distancia) en la dirección de  , la cual se llama derivada direccional de
, la cual se llama derivada direccional de en la dirección de
en la dirección de  .
.
VECTOR GRADIENTE
un punto genérico  del dominio de
del dominio de  ,
,  (
( ), indica la
dirección en la cual el campo
), indica la
dirección en la cual el campo  varía más rápidamente y su
módulo representa el ritmo de variación de
varía más rápidamente y su
módulo representa el ritmo de variación de  en la dirección
de dicho vector gradiente. El gradiente se representa con el
operador diferencial nabla
en la dirección
de dicho vector gradiente. El gradiente se representa con el
operador diferencial nabla  seguido de la función (cuidado
se denota con un punto de producto escalar entre el
operador nabla y el campo). También puede representarse
mediante
seguido de la función (cuidado
se denota con un punto de producto escalar entre el
operador nabla y el campo). También puede representarse
mediante  , o usando la notación
, o usando la notación  . La generalización
del concepto de gradiente a campos
. La generalización
del concepto de gradiente a campos  vectoriales es el
vectoriales es el
 del dominio de
del dominio de  ,
,  (
( ), indica la
), indica la  varía más rápidamente y su
varía más rápidamente y su  en la dirección
en la dirección  seguido de la función (cuidado
seguido de la función (cuidado  , o usando la notación
, o usando la notación  . La generalización
. La generalización  vectoriales es el
vectoriales es el Definición
Se toma como campo escalar el que se asigna a cada punto
del espacio una presión P (campo escalar de 3 variables),
entonces el vector gradiente en un punto genérico del
espacio indicará la dirección en la cual la presión cambiará
más rápidamente. Otro ejemplo es el de considerar el mapa
de líneas de nivel de una montaña como campo escalar,
que asigna a cada pareja de coordenadas latitud/longitud un
escalar altitud (campo escalar de 2 variables). En este caso
el vector gradiente en un punto genérico indicará la
dirección de máxima inclinación de la montaña. Nótese que
el vector gradiente será perpendicular a las líneas de
contorno (líneas "equiescalares") del mapa. El gradiente se
define como el campo vectorial cuyas funciones
coordenadas son las derivadas parciales del campo escalar,
esto es:

Esta definición se basa en que el gradiente permite calcular
fácilmente las derivadas direccionales. Definiendo en primer
lugar la derivada direccional según un vector:

Una forma equivalente de definir el gradiente es como el
único vector que, multiplicado por el vector unitario, da la
derivada direccional del campo escalar:

Con la definición anterior, el gradiente está caracterizado de
forma unívoca. El gradiente se expresa alternativamente





Interpretación del gradiente
De forma geométrica el gradiente es un vector que se
encuentra normal (perpendicular) a la curva de nivel en el
punto que se está estudiando, llámese (x,y), (x,y,z), (tiempo,
temperatura), etcétera. Algunos ejemplos son:
- Considere una habitación en la cual la temperatura se define a través de un campo escalar, de tal manera que en cualquier punto
 , la temperatura es
, la temperatura es  . Asumiremos que la temperatura no varía con respecto al tiempo. Siendo esto así, para cada punto de la habitación, el gradiente en ese punto nos dará la dirección en la cual la temperatura aumenta más rápido. La magnitud del gradiente nos dirá cuan rápido aumenta la temperatura en esa dirección.
. Asumiremos que la temperatura no varía con respecto al tiempo. Siendo esto así, para cada punto de la habitación, el gradiente en ese punto nos dará la dirección en la cual la temperatura aumenta más rápido. La magnitud del gradiente nos dirá cuan rápido aumenta la temperatura en esa dirección.
- Considere una montaña en la cual su altura en el punto (x,y) se define como H(x, y). El gradiente de H en ese punto estará en la dirección para la que hay un mayor grado de inclinación. La magnitud del gradiente nos mostrará cuán empinada se encuentra la pendiente.
 , la temperatura es
, la temperatura es  . Asumiremos que la temperatura no varía con respecto al tiempo. Siendo esto así, para cada punto de la habitación, el gradiente en ese punto nos dará la dirección en la cual la temperatura aumenta más rápido. La magnitud del gradiente nos dirá cuan rápido aumenta la temperatura en esa dirección.
. Asumiremos que la temperatura no varía con respecto al tiempo. Siendo esto así, para cada punto de la habitación, el gradiente en ese punto nos dará la dirección en la cual la temperatura aumenta más rápido. La magnitud del gradiente nos dirá cuan rápido aumenta la temperatura en esa dirección.Propiedades
El gradiente verifica que:
- Es ortogonal a las superficies equiescalares, definidas por
 =cte.
=cte.
- Apunta en la dirección en que la derivada direccional es máxima.
- Su norma es igual a esta derivada direccional máxima.
- Se anula en los puntos estacionarios (máximos, mínimos y puntos de silla).
- El campo formado por el gradiente en cada punto es siempre irrotacional, esto es,

 =cte.
=cte.
A partir de su definición puede hallarse su expresión en
cartesianas, su expresión es simplemente

En un sistema de coordenadas ortogonales, el gradiente
requiere los factores de escala, mediante la expresión



En un sistema de coordenadas curvilíneo general el
gradiente tiene la forma:

donde en la expresión anterior se usa el convenio de





Gradiente de un campo vectorial
En un espacio euclidiano tridimensional, el concepto de
gradiente también puede extenderse al caso de un campo
vectorial, siendo el gradiente de  un tensor que da el
diferencial del campo al realizar un desplazamiento:
un tensor que da el
diferencial del campo al realizar un desplazamiento:

Fijada una base vectorial, este tensor podrá representarse
por una matriz 3x3, que en coordenadas cartesianas está
formada por las tres derivadas parciales de las tres
componentes del campo vectorial. El gradiente de
deformación estará bien definido sólo si el límite anterior
existe para todo  y es una función continua de dicho vector.
y es una función continua de dicho vector.
Técnicamente el gradiente de deformación no es otra cosa
que la aplicación lineal de la que la matriz jacobiana es su
expresión explícita en coordenadas.
 un tensor que da el
un tensor que da el 
 y es una función continua de dicho vector.
y es una función continua de dicho vector.Ejemplos
1. Dada la función  su vector gradiente es el siguiente:
su vector gradiente es el siguiente:

2. Dada la función  su vector gradiente es el siguiente:
su vector gradiente es el siguiente:

3. Dada la función  su vector gradiente es el siguiente:
su vector gradiente es el siguiente:

 su vector gradiente es el siguiente:
su vector gradiente es el siguiente:
 su vector gradiente es el siguiente:
su vector gradiente es el siguiente:
 su vector gradiente es el siguiente:
su vector gradiente es el siguiente:
Aplicaciones
Aproximación lineal de una función
El gradiente de una función  definida
función en un punto particular
definida
función en un punto particular  en Rn. Se expresa así:
en Rn. Se expresa así:
 donde
donde  es el
es el
gradiente evaluado en 
 definida
definida  en Rn. Se expresa así:
en Rn. Se expresa así: donde
donde  es el
es el
gradiente evaluado en 

Aplicaciones en física
La interpretación física del gradiente es la siguiente: mide
la rapidez de variación de una magnitud física al
desplazarse una cierta distancia. Un gradiente alto significa
que de un punto a otro cercano la magnitud puede presentar
variaciones importantes (aquí se entiende por gradiente alto
o grande uno tal que su módulo es grande). Un gradiente de
una magnitud pequeño o nulo implica que dicha magnitud
apenas varía de un punto a otro.
El gradiente de una magnitud física posee innumerables
aplicaciones en física, especialmente
en electromagnetismo y mecánica de fluidos. En particular,
existen muchos campos vectoriales que puede escribirse
como el gradiente de un potencial escalar.
- Uno de ellos es el campo electrostático, que deriva del potencial eléctrico:

- Todo campo que pueda escribirse como el gradiente de un campo escalar, se denomina potencial, conservativo o irrotacional. Así, una fuerza conservativa deriva de la energía potencial como:

- Los gradientes también aparecen en los procesos de difusión que verifican la ley de Fick o la ley de Fourier para la temperatura. Así, por ejemplo, el flujo de calor en un material es directamente proporcional al gradiente de temperaturas

- siendo
 la conductividad térmica.
la conductividad térmica.



 la conductividad térmica.
la conductividad térmica.
Maximos y Minimos
Si f está una función de x y y, entonces f tiene un máximo relativo a (a, b) si f(a, b) ³ f(x, y) para toda (x, y) en una pequeña cercanía de (a, b). Un mínimo relativo se define en manera parecida. f tiene un punto de silla en (a, b) si f tiene allí un mínimo relativo a lo largo de un corte y un máximo relativo a lo largo de un otro corte.
La función que se ilustra mas abajo tiene un mínimo relativo a (0, 0), un máximo relativo a (1, 1), y puntos de silla a (1, 0) y (0, 1).

En los casos que estudiamos, todos extremos relativos y puntos de silla que no sean en la frontera del dominio de f se ocurren a puntos críticos, que son las soluciones de las ecuaciones
- fx(x,y) = 0
y
- fy(x,y) = 0.
Prueba de segunda derivada para funciones de dos variables
Si f(x, y) está una función de dos variables, y (a, b) es un punto crítico de f. (Esto es, fx(a, b) = 0 y fy(a, b) = 0.) Suponga también que existen y son iguales las derivadas del segundo orden, de modo que, por teoremas de cálculo, fxy es igual a fyx. Sea
- H = fxx(a, b)fyy(a, b) -[fxy(a, b)]2.
Entoncesf tiene un mínimo relativo a (a, b) si H > 0 y fxx(a,b) > 0,
f tiene un máximo relativo a (a, b) si H > 0 y fxx(a,b) < 0, y
f tiene un punto de silla a (a, b) si H < 0.
Si H = 0 la prueba no dice nada, entonces necesitamos analizar la gráfica para buscar más información.

Si f(x, y) está una función de dos variables, y (a, b) es un punto crítico de f. (Esto es, fx(a, b) = 0 y fy(a, b) = 0.) Suponga también que existen y son iguales las derivadas del segundo orden, de modo que, por teoremas de cálculo, fxy es igual a fyx. Sea
f tiene un máximo relativo a (a, b) si H > 0 y fxx(a,b) < 0, y
f tiene un punto de silla a (a, b) si H < 0.
Máximos y mínimos restringidos
Un problema restringido de optimización Tiene la forma
- Maximiza (o minimiza) f(x, y,. . . ) sujeta a restricciones.
Las restricciones están en forma de ecuaciones o en forma de restricciones del dominio de f. Podemos resolver estos problemas por primero despejar una de las variables de las ecuaciones de restricción, para después sustituirla en f, y después ubicar el máximo (o mínimo) de la función que resulta. En casos en los que el dominio R de la función resultando tiene una frontera, tenemos también ubicar los extremos de f cuando se está restringido a la frontera.
Multiplicadores de Lagrange
Para localizar los candidatos a extremos relativos de una función f(x, y, . . .) sujeta a la restricción g(x, y, ...) = 0, se resuelve el siguiente sistema de ecuaciones para obtener x, y, ... y λ:
- fx = λgx
- fy = λgy
- ...
- g = 0
El incógnita λ se llama un multiplicador de Lagrange. Los puntos (x, y, . . .) que se ocurren in las soluciones son los candidatos a los extremos relativos de la función f sujeta a g = 0.
Para localizar los candidatos a extremos relativos de una función f(x, y, . . .) sujeta a la restricción g(x, y, ...) = 0, se resuelve el siguiente sistema de ecuaciones para obtener x, y, ... y λ:
Ejemplos
1. Sea f(x, y) = x2 - (y-1) 2. Entonces fx(x,y) = 2x; fy(x, y) = -2(y-1). Para encontrar los puntos críticos, resolvemos la sistema
2x = 0
-2(y-1) = 0.
La primera ecuación produce x = 0, y la segunda da y = 1. Entonces, el único punto crítico es (0, 1). Como el dominio de f es el plano cartesiano entero, entonces el punto (0, 1) es interior, y entonces es un candidato a ser un extremo relativo o punto de silla.
Para comprobar cual, calcule primero las derivadas segundas:
fxx(x, y) = 2
fyy(x, y) = -2
fxy(x, y) = fyx(x, y) = 0
Después calcule
H = fxx(0, 1)fyy(0, 1) -[fxy(0, 1)]2 = (2)(-2) -02 =- 4
Como H es negativo, tenemos un punto de silla a (0, 1). Aquí está la gráfica de f que muestra su ubicación.

-2(y-1) = 0.
fyy(x, y) = -2
fxy(x, y) = fyx(x, y) = 0
| H | = | fxx(0, 1)fyy(0, 1) -[fxy(0, 1)]2 |
| = | (2)(-2) -02 =- 4 |

Criterio de la segunda derivada
Sea f(x,y) con sus primeras y segundas derivadas
parciales contínuas en un disco con centro en (a,b)
y además fx(a,b) = 0 y
fy(a,b) =0.
- Si D > 0 y fxx(a,b) > 0, entonces f(a,b) es un mínimo local.
- Si D > 0 y fxx(a,b) < 0, entonces f(a,b) es un máximo local.
- Si D < 0 en (a,b), entonces f(a,b) es un punto silla.
- Si D = 0 en (a,b), el criterio no decide. En este caso debemos buscar otra forma de determinar el comportamiento de f en (a,b).
D, se conoce como discriminante o Hessiano de f.
Otra forma: D = fxx(a,b) fyy(a,b) – fxy(a,b) fyx (a,b)
Sea f(x,y) con sus primeras y segundas derivadas
parciales contínuas en un disco con centro en (a,b)
y además fx(a,b) = 0 y
fy(a,b) =0.
- Si D > 0 y fxx(a,b) > 0, entonces f(a,b) es un mínimo local.
- Si D > 0 y fxx(a,b) < 0, entonces f(a,b) es un máximo local.
- Si D < 0 en (a,b), entonces f(a,b) es un punto silla.
- Si D = 0 en (a,b), el criterio no decide. En este caso debemos buscar otra forma de determinar el comportamiento de f en (a,b).
D, se conoce como discriminante o Hessiano de f.
Otra forma: D = fxx(a,b) fyy(a,b) – fxy(a,b) fyx (a,b)
Integrales Múltiples
Integrales Iteradas
Se llaman integrales iteradas a la realización sucesiva de por lo menos 2 procesos de integración simple considerando las diferenciales dx y dy.
Es importante tomar en cuenta en que posición vienen dados los límites de las integrales en cuestión para saber en que orden serán ejecutados los procesos de integración simple; es decir, reconocer si se va integrar primero considerando la diferencial dx o la diferencial dy o viceversa.
FORMAS EN QUE PUEDEN PRESENTARSE LAS INTEGRALES ITERADAS


Área por Doble Integración
La aplicación más simple de las integrales dobles es para hallar el área de una región del plano xy. Esta área esta dada por una cualquiera de las integrales

Los límites de integración apropiados. Ya hemos visto como se hace esto en la figura 1, cuando se efectúan las integraciones primero respecto a y, y después respecto a x; es decir

Esta última integral podía haberse escrito de primera intención, puesto que expresa el área como límite de la suma de fajas horizontales.
Integrales dobles
Definición geométrica de la integral doble
La integral doble de f(x, y) en la región R del plano xy se define como


R f(x, y) dx dy
= Volumen arriba de la región R y abajo de la gráfica de f
- Volumen abajo de la región R y arriba de la gráfica de f.
La siguiente figura demuestra el volumen (en el caso que la gráfica de f está arriba de la región R).

Calculación de integrales dobles
Si R es el rectángulo a ≤ x ≤ b y c ≤ y ≤ d (vea la figura más abajo) entonces


R f(x, y) dx dy = 
d
c 

b
a f(x, y) dx 
dy = 
b
a 

d
c f(x, y) dy 
dx

Si R es la región a ≤ x ≤ b y c(x) ≤ y ≤ d(x) (como se demuestra en la figura más abajo) entonces se calcula la integral en R con la siguiente ecuación:


R f(x, y) dx dy = 
b
a 

d(x)
c(x) f(x, y) dy 
dx

Si R es la región c ≤ y ≤ d y a(y) ≤ x ≤ b(y) (como se demuestra en la figura más abajo) entonces se calcula la integral en R con la siguiente ecuación:


R f(x, y) dx dy = 
d
b 

b(y)
a(y) f(x, y) dx 
dy

La integral doble de f(x, y) en la región R del plano xy se define como
| R | f(x, y) dx dy |
| = Volumen arriba de la región R y abajo de la gráfica de f - Volumen abajo de la región R y arriba de la gráfica de f. |

Si R es el rectángulo a ≤ x ≤ b y c ≤ y ≤ d (vea la figura más abajo) entonces
| R | f(x, y) dx dy = | d c | b a | f(x, y) dx | dy | |||||
| = | b a | d c | f(x, y) dy | dx |

| R | f(x, y) dx dy = | b a | d(x) c(x) | f(x, y) dy | dx |

| R | f(x, y) dx dy = | d b | b(y) a(y) | f(x, y) dx | dy |

Ejemplos
Si R es el rectángulo 1 ≤ x ≤ 2 y 1 ≤ y ≤ 3, entonces


R x dx dy =

3
1 

2
1 x dx 
dy
=

3
1 
3

2

dy
= 3
Sea R la región definida por 0 ≤ x ≤ 2, 0 ≤ y ≤ x (vea la figura)



R x dx dy =

2
0 

x
0 x dy 
dx
=

2
0 
xy 
x
y=0 dx
=

2
0 x2 dx =
8

3
Sea R la misma región que lo más arriba, pero esta vez descrita por 0 ≤ y ≤ 2, y ≤ x ≤ 2 (vea figura)



R x dx dy =

2
0 

2
y x dx 
dy
=

2
0 
x2

2

2
x=y dy
=

2
0 
2 -
y2

2

dy =
8

3
| R | x dx dy = |
| |||||||||
| = |
| = 3 |

| R | x dx dy = |
| |||||||||
| = |
| ||||||||||
| = |
|

| R | x dx dy = |
| ||||||||||
| = |
| |||||||||||
| = |
|
Integrales dobles como volúmenes
Cuando f(x ,y) es positiva podemos interpretar la integral doble de f sobre una región rectangular R como el volumen del prisma sólido limitado abajo por R y arriba por la superficie z = F(x, y). Cada termino f (xk, yk)
"Ak en la suma Sn = 

"Ak es el volumen de un prisma rectangular vertical que aproxima el volumen de la porción del sólido que está directamente arriba de la base "Ak. La suma Sn aproxima entonces a lo que llamamos volumen total del sólido. Definido este volumen como

Coordenadas Polares
En un espacio R2, un dominio de integración que tenga una simetría circular es muchas veces suceptible de ser transformado de coordenadas rectangulares a polares, lo que significa que cada punto P (x, y) del dominio de una integral doble tomará su valor correspondiente en coordenadas polares mediante la siguiente transformación:

Por ejemplo:

Si aplica la identidad trigonométrica pitagórica de senos y cosenos.
El determinante jacobiano de la transformación es:

Definición Integral triple
Es la aplicación sucesiva de tres procesos de integración definida simple a una función de tres variables f (x, y, z); tomando en consideración en función de que variable se encuentran los límites para saber cual diferencial (dx, dy, dz) se utilizará primero y cual después y cual al final.
Ejemplo.

Integrales Triples en Coordenadas Cilíndricas y Esféricas
Coordenadas cilíndricas.
Las coordenadas cilíndricas son apropiadas para describir cilindros cuyos ejes coinciden con el eje x y planos que contienen el eje z o bien son perpendiculares a el.
r = 4 Cilindro, radio 4, eje el eje z

Plano que contiene al eje z
z= 2 Plano perpendicular al eje z
El elemento de volumen para subdividir una región en el espacio con coordenadas cilíndricas es

Las integrales triples en coordenadas cilíndricas son entonces evaluadas como integrales iteradas, como el siguiente ejemplo.
EJEMPLO.

Solución
Paso 1: La base de D también es la proyección de la región R sobre el plano xy. La frontera de R es el
círculo

Su ecuación en coordenadas polares es

Paso 2: Los límites z de integración. Una recta M, que pasa por un punto típico (r,  ) en R, paralela al eje z, entra a D en z=0 y sale en
) en R, paralela al eje z, entra a D en z=0 y sale en
 ) en R, paralela al eje z, entra a D en z=0 y sale en
) en R, paralela al eje z, entra a D en z=0 y sale en
Paso 3: Los límites r de integración. Un rayo L que pasa por (r, ) desde el origen, entra a R en r =0 y sale en
Paso 4: Los límites de integración. Al barrer L a través de R, el ángulo que forma con el eje x positivo varía de La integral es
Coordenadas esféricas.
Las coordenadas esféricas son apropiadas para describir con centro en el origen, medios planos articulados a lo largo de eje z y conos simples, cuyos vértices se encuentran en el origen, y con ejes a lo largo del eje z.
Las superficies como ésas tienen ecuaciones de valor coordenado constante:

EJEMPLO.
El volumen es

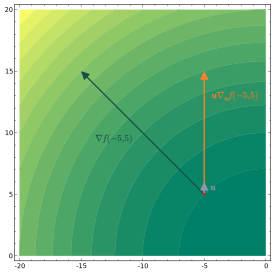
 , mostrando el vector gradiente en azul, y el vector unitario
, mostrando el vector gradiente en azul, y el vector unitario 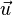 escalado por la derivada direccional en la dirección de
escalado por la derivada direccional en la dirección de 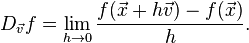

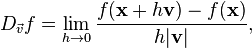














 ,
,  ) resulta
) resulta ,
,  ,
,  )
)






0 comentarios:
Publicar un comentario